解一下山羊吃草问题

2021-05-28

问题定义

哪里看到的

　看到这个问题是在阮一峰的周报《科技爱好者周刊（第 160 期）：中年码农的困境》（备用链接）。他的文章又指向了原网页 How to Solve Equations That Are Stubborn as a Goat。原网页以及阮一峰的文章都由简到难讨论了不同种情况羊可以吃到的草的面积。

　对于本文所要解决的问题，原文章里属于「学有余力的同学课后自己做一下」的类型。所以我就单独写了这篇 Blog。

定义

　有一个圆形围栏的牧场。有一只羊拴在牧场里面。

（图片来源：https://www.quantamagazine.org/）

　问拴绳是多长的时候，羊吃到的牧草的面积占圆形草场面积的一半？

（图片来源：https://www.quantamagazine.org/）

　是不是看起来挺简单？这个问题 已经出现了两百多年了，而且直到2020 年 2 月才有一位德国数学家 Ingo Ullisch 给出了 解析解（Closed-form expression）。之前人们也有答案，但是只能用数值计算的方法给出近似解。

　求出近似解也不那么难。大家也可以想一想，我加点空行分割一下。

我的解法

　其实要得到最后的方程最多也就用到高中平面几何的知识。只不过一题可以多解，所以才有讨论的空间。

　第一步，把问题抽象成两个圆。

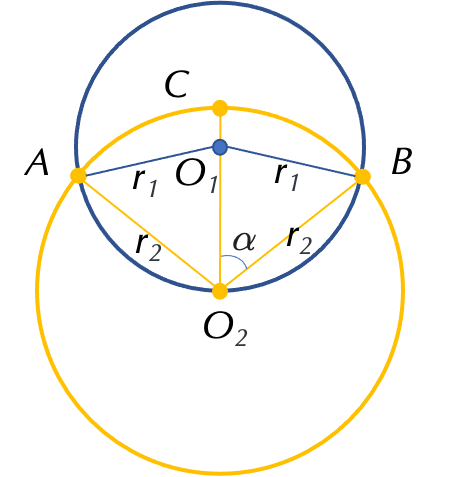
　草场的圆心是 $O_1$，羊活动的圈子的圆心是 $O_2$。两圆的交点为 $A$ 和 $B$ 。$C$ 是两圆心连线和 $\odot O_2$ 的交点。

　可以得出以下等量关系：

且 $0<r_2<2r_1$。

　想求面积可以按下面的划分方法进行计算。如果按照不同的划分方法可能会得到不一样的形式。

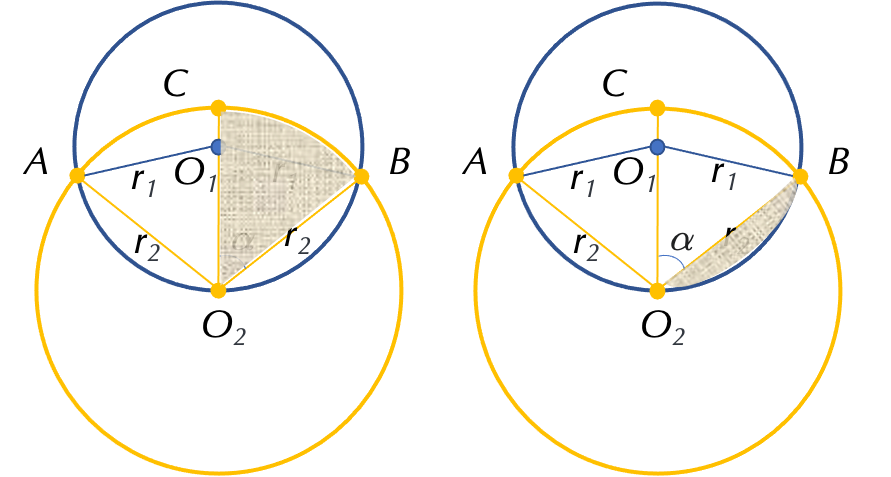
　先求出上左图扇形 $O_2BC$ 的面积 $S_{\text{Sec1}}$，再求出上右图的 $O_2B$ 和 $\odot O_1$ 所围成区域的面积 $S_{\text{Sec2}}$，把两者加起来再乘以 2，让表达式等于 $\odot O_1$ 面积的一半即可。

　可通过以下方式求得 $S_{\text{Sec2}}$：

　第一项扇形面积好弄，主要是要求出等腰三角形 $\triangle O_1O_2B$ 的面积。为此我们需要计算 $\alpha$ 和 $\beta=\angle O_2O_1B$ 的大小。

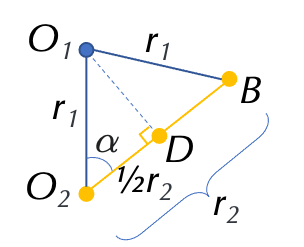
　由简单的几何关系可知：

　三角形的面积可以用经典的「底乘以高除以二」，但是高 $O_1D$ 的表达式 $h = \sqrt{r_1^2-(\frac{r_2}{2})^2}$ 有点复杂。我们也可以用三角函数求面积：

　（备注：把 $\sin\arccos x$ 化简以后其实和底乘以高除以二的形式是一样的。）

　写出 $S_{\text{Sec1}}$ 和 $S_{\text{Sec2}}$ 的表达式：

　列出方程：

　带入各项：

　显然，$\frac{r_2}{r_1}$ 对于不同的圆来说都是一样的（有相似性），所以我们令 $r_1=1$，得到：

　令

　只需求解函数 $f(r_2)=0$ 的根即为最终答案。

　我们先画出 $f(r_2)$ 的样子看看长啥样。右图是局部放大。

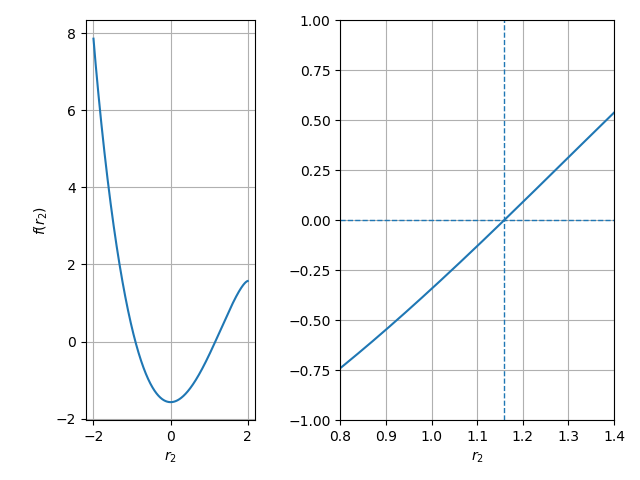
　但是从函数的表达式可知这是一个超越方程（Transcendental equation），类似 $x=\cos(x)$，我们是不可能得到闭式解的。所以我们就用计算机帮我们找 $f(r_2)$ 和 $x$ 轴的交点即可。以前这种问题都是扔到 MatLab 里面跑一下就出来了。由于好久没用 MatLab了，这次我用 Python。

　写点代码：

import numpy as np
from scipy.optimize import fsolve

def calculate_f(r):
    term1 = (np.square(r) - 2) * np.arccos(r / 2)
    term2 = 1 / 2 * np.pi - r * np.sin(np.arccos(r / 2))
    f = term1 + term2
    return f

def scipy_solve():

    r_initial_guess = 1
    return fsolve(calculate_f, r_initial_guess)

res = scipy_solve()
print(res)

　跑一下可知。答案是 $r_2=1.15872847$，一个看起来没有啥规律的数。硬要说的话大概和 $\pi-2$ 很接近。

　到这里就全部解决了。这个问题不算难，不过对我来说意义更大的是把「问题抽象 - 公式化 - 数值计算」这个流程走了一遍，把很多很久不用的知识串联了一下。温故而知新。

　下面是一些我写这个文章的时候搜到的其他方法和拓展。大部分来自 Goat Problem - WikiPedia 和 @量子位 的微信公众号文章。

透镜面积公式

　两个圆重叠的部分正好是一个光学透镜，透镜的面积似乎是有现成的公式的。具体过程省略，但是最后是这样的：

　令 $f_2(r_2)=0$ 算出来的结果和上面的是一样的。但是有意思的是，这个函数的曲线在 $x\geq0$ 的部分和我的是一样的，但是 $x<0$的部分则有显著的不同。见下图：

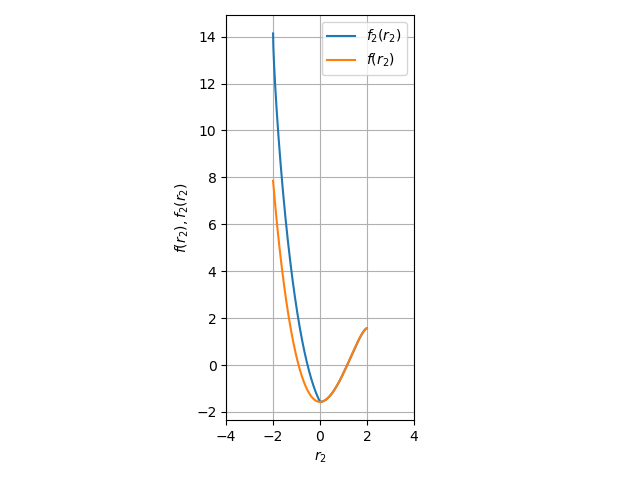
　这两个函数都是连续的，但是 $f_2(r_2)$ 在 $x=0$ 处是不可导的，因为不光滑。不过因为有 $r_2>0$ 的限制，所以这个差别就无所谓了。

　除了透镜面积解法，还有一种 积分法 获得方程的解法。这里就省略了。

解析解

　这个就是德国数学家找到的方法。过程我没看（反正也看不懂），大概用到了 Complex analysis 和复变函数，早就忘光了。直接放维基百科上的结果吧：

　这个表达式想要得到数值解也还是得用计算机。不过解析解和数值解在数学上还是有着很不一样的意义的。前者标志着人们已经几乎从根本上认识和解决了这个问题。

飞鸟问题：山羊问题的三维化

　数学家们还在研究三维球体的类似规律： 一只鸟被拴在一个球体笼子内部的一个点上，问半径多少的时候鸟的活动范围的体积是这个球体积的一半？

　这个问题的模型就像把上面 $O_1$ 和 $O_2$ 绕对称轴旋转一圈形成的球体。

（图片来源：Goat Problem - WikiPedia）

　但是从二维到三维不具有相似性。这个绳长需要更长一些才能满足要求。WikiPedia 上用棱镜体积公式得到如下方程：

　$f_3(r)=-\frac{1}{4}\pi r^4+\frac{2}{3}\pi r^3 - \frac{2}{3}\pi$ 的曲线如下：

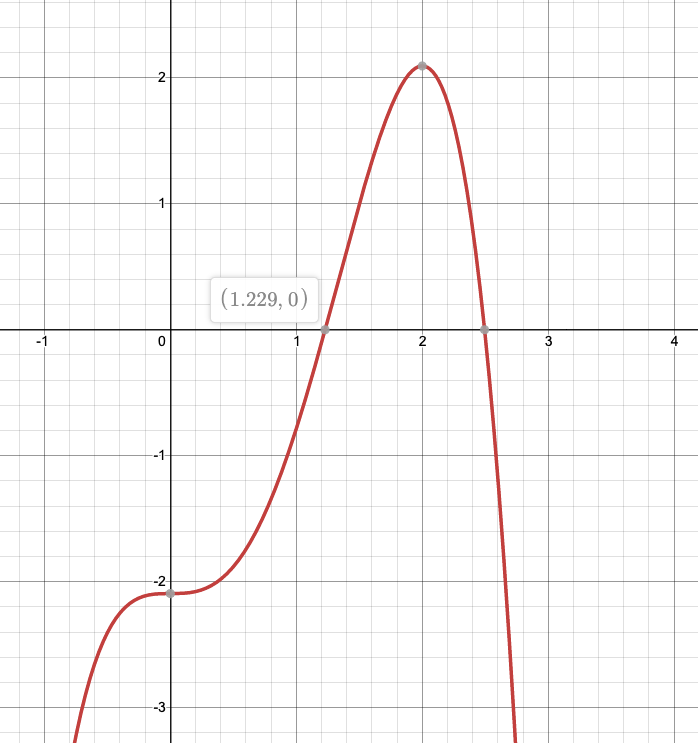（图片来源：用 desmos 画的）

　这个方程（一元四次方程）显然比二维问题的时候舒服很多，没有三角函数项了。不过四次方程的求根公式异常复杂。大约还没有人真正算出解析解的表达式吧。用数值计算法的话倒是可以轻松得到答案 $r=1.2285$。

　这个问题解决了。

高维怪物问题：山羊问题的高维化

　数学家们最擅长干这个：把二维、三维的问题继续推广到高维，求出半径 $r$ 与维度 $n$ 的关系。这样有助于我们从根本上理解这个问题。

　假设有个高维生物拴在一个高维球体的内部，请问绳长是多少的时候，高维生物的活动范围是高维球体「体积」的一半？

　具体表达式好像也没有，但是规律是，如果维度 $n$ 趋向于无穷，那么半径 $r$ 趋向于 $\sqrt{2}=1.4142…$。从二维到三维也可以看出一些端倪。二维的时候 $r=1.129$，三维是 $r=1.2285$。随着维度增加，需要的半径总会是越来越大的。

数学

　很多人对这种问题也表示不解：研究它有啥用？

　数学如果能率先发展那么就可以作为其他领域发展的工具或基石。历史上有很多例子是物理学发展到一定程度停滞了，需要等数学进一步发展才能反过来推动的。很多时候数学研究的问题还没有即时的工程应用上的参照，但是我们不应该囿于当下人们对世界的表面认识。把理论的疆域拓展了才能让人类的可能性进一步提高。

在最后的声明

　我还有点搞不清「解析解」和「闭式解」的 区别。如果谁清楚的话可以解释一下。

　很久没用数学的语言了，另外，打这些 LaTeX 公式挺费劲的，如果发现文章有问题欢迎指正。

LanternD